MatheGrafix 12 / Online-Hilfe

Eingabe und Bearbeitung einer Formel - Beispiel: y = mx+b

1. Eingabe der Formel y = mx+b und die Schreibweise in MatheGrafix

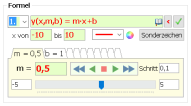Die linke Seite der Formel: Auf der linken Seite einer Formel benötigt MatheGrafix einen Funktionsnamen, hier bieten sich y oder f an.
Die Formel y=mx+b enthält die Variable x und die Parameter m und b. Um MatheGrafix diesen Sachverhalt mitzuteilen, schreibt man hinter den Funktionsnamen zuerst die Variable und dann die Parameter in Klammern, man erhält also für die linke Seite der Formel y(x,m,b). MatheGrafix kann bis zu 10 Parameter verarbeiten.

Die rechte Seite der Formel: Auf der rechten Seite der Formel fügt man noch das Zeichen * oder das neue Sonderzeichen ∙ für die Multiplikation ein. Die fertige Schreibweise der Formel in Mathegrafix ist demnach
y(x,m,b) = m∙x + b oder auch f(x,m,b) = m*x + b.

2. Festlegen des Definitionsbereichs für die Variable x

Den Definitionsbereich der Formel (x von ... bis) für die Variable x legt man in den Eingabefeldern direkt unter (oder im Vollbild neben) dem Eingabefeld für die Formel fest.

3. Ändern der Werte für die Parameter m und b

Durch die Eingabe y(x,m,b) auf der linken Seite der Formel erzeugt MatheGrafix automatisch eine Tabelle für die Parameter mit den Reitern m und b.
Den Wert einen Parameters in der Tabelle kann man auf drei Arten verändern:

• durch die Eingabe des Wertes direkt in das Eingabefeld für den Parameter.
• mit dem Schieberegler zum Parameter - man kann die linke Grenze, rechte Grenze und die Schrittweite für den Schieberegler festlegen.
• Über das Bedienfeld  " << < ▢ > >> " kann man den Schieberegler automatisch schnell oder langsam laufen lassen. Damit wird der Wert des jeweiligen Parameters automatisch geändert und seine Wirkung gezeigt.
  Siehe dazu auch die ausführliche → Hilfeseite Formel - Schieberegler!

4. Anzeige der Funktion - die Einheiten der Achsen und die Lage des Ursprungs

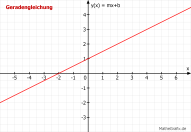Im rechten Fenster lassen sich die Einheiten der Achsen mit den Schiebereglern im Eingabefeld Achsen einstellen. Die Länge der Achsen kann direkt in "cm" eingestellt werden.
Die Lage des Ursprungs im Koordinatensystem verschiebt man mit Drag & Drop.

5. Funktionenschar einer Formel

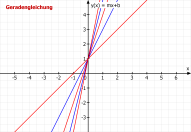Durch das Umschalten des Reiters "Formel" auf den Reiter "Funktion" erhält
man unmittelbar eine Funktionenschar dieser Formel.
Beim Umschalten bleiben alle Werte für die Parameter erhalten bis auf den ersten Parameter, bei der Geradengleichung y(x,m,b) = ist das m. Dieser Parameter m wird für die Funktionenschar verwendet:
Im Modul "Formel" ist m=0,5,
beim Umschalten auf "Funktion" erhält man m = 1 bis 5, Schritt 1.

6. Das fertige Beispiel

Das fertige Beispiel "Geradengleichung" findet man in MatheGrafix direkt unter dem Eingabefeld für die Formel im Feld "Beispiele" und in der Datei geradengleichung.mg12