MatheGrafix 12 / Online-Hilfe

Vorbemerkungen

Einen schnellen Überblick über die Möglichkeiten des Moduls "Normalverteilung" erhält man mit den Beispielen im linken Fenster von MatheGrafix: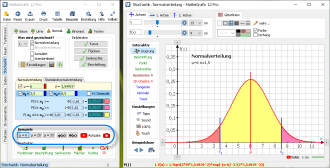
Die Beispiele zeigen

1. die Dichtefunktion der Normalverteilung mit dem Erwartungswert µ=6 und der Standardabweichung σ≈1,5 mit markierten Flächen,
2. die Dichtefunktion der Normalverteilung mit dem Erwartungswert µ=20 und der Standardabweichung σ≈3,5 ohne Markierung der Flächen und
3. die Verteilungsfunktion der Normalverteilung mit dem Erwartungswert µ=33 und der Standardabweichung σ≈4,7.

Eigenschaften und Einstellungen der Normalverteilung in MatheGrafix

1. Das Feld "Was wird gezeichnet?"

Zum Ausprobieren wählt man das Beispiel mit µ=6 im linken Fenster von MatheGrafix.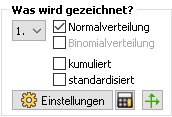
Im Feld "Was wird gezeichnet?" findet man verschieden Einstellmöglichkeiten:

• Man sollte die Binomialverteilung ausgeblendet lassen!
• Setzt man nun ein Häkchen bei kumuliert, erhält man statt der Dichtefunktion die Verteilungsfunktion.
• Setzt man ein Häkchen bei standardisiert, wird die Normalverteilung einschließlich der Grenzen x₁ und x₂ in die Standardnormalverteilung mit den Grenzen z₁ und z₂ übertragen. Dies erreicht man allerdings auch, indem man im Rechenfeld darunter den Reiter "Standardnormalverteilung" wählt.

• Mit dem Button, der ein grünes Koordinatensystem zeigt, werden die Koordinatenachsen automatisch angepasst. Ist er gedrückt, wird diese Automatik ausgeschaltet.
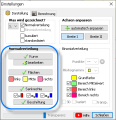
• Mit dem Button "Einstellungen" gelangt man zu einem erweiterten Einstellfenster (siehe rechts).

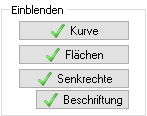
2. Das Feld "Einblenden"

In diesem Feld kann man ein- oder ausblenden:

• die Kurve der Normalverteilung,
• die Fläche zwischen Kurve und waagerechter Achse,
• die Senkrechten mit ihrer Beschriftung oder
• nur die Beschriftung der Senkrechten.

3. Das Feld zur Berechnung von Normalverteilung und Standardnormalverteilung

Die Genauigkeit entspricht exakt den ablesbaren Tabellenwerten einer Formelsammlung und macht damit die Verwendung der Tabellen aus einer Formelsammlung überflüssig!

• Unter dem Reiter "Normalverteilung" gibt man die bestimmenden Größen Erwartungswert µ und die Standardabweichung σ ein.
• Im blauen Feld darunter legt man die Grenzen x₁ und x₂ fest. Setzt man ein Häkchen bei "+1 Dezimale", erhöht sich die Rechengenauigkeit gegenüber den üblichen ablesbaren Tabellenwerten einer Formelsammlung um eine Stelle.
• Hier kann man auch ein Häkchen für die Zeichnung der Senkrechten µ, x₁ und x₂ setzen sowie deren Farbe bestimmen.
• Im etwas helleren Rechenfeld darunter wird die Wahrscheinlichkeit der drei Bereiche berechnet, die durch die Senkrechten x₁ und x₂ getrennt werden. Außerdem lassen sich hier noch die Farben der Bereiche einstellen.

Klickt man auf den Reiter "Standardnormalverteilung", wird die aktuelle Normalverteilung auf die Standardnormalverteilung mit µ=0 und σ=1 übertragen. Die Grenzen x₁ und x₂ werden dabei zu z₁ und z₂ transformiert.

In zwei weiteren Beispielen können die Dichtefunktion φ(x) und die Verteilungsfunktion Φ(x) der Standardnormalverteilung direkt betrachtet und deren Bereiche berechnet werden.