MatheGrafix 12 / Online-Hilfe

Vorbemerkungen

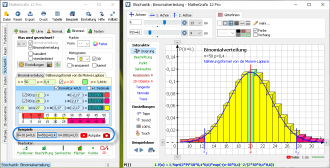Einen Überblick über die Möglichkeiten des Moduls "Binomialverteilung" erhält man mit den Beispielen:

1. Beispiel: Mit n=10 und p=0,6 wird die Binomialverteilung mit Rechtecken dargestellt.
2. Beispiel: Mit n=50 und p=0,4 erfolgt die Darstellung mit Quadern. Zusätzlich wird die entsprechende
   Kurve der Normalverteilung mit µ=20 und σ=3,4641 automatisch erzeugt und gezeichnet.
3. Beispiel: Mit n=100 und p=1/3 wird eine kumulierte Binomialverteilung gezeigt.

Eigenschaften und Einstellungen der Binomialverteilung in MatheGrafix

1. Das Feld "Was wird gezeichnet?"

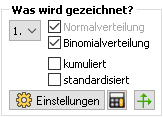Zum Ausprobieren wählt man das Beispiel mit n=50.
Im linken Fenster im Feld "Was wird gezeichnet?"
findet man verschieden Einstellmöglichkeiten.

• Die Kurve der automatisch berechneten Normalverteilung lässt sich einblenden.
• Mit dem jeweiligen Häkchen lässt sich die Binomialverteilung kumuliert und standardisiert darstellen.
• Mit dem Button, der ein grünes Koordinatensystem zeigt, werden die Koordinatenachsen automatisch angepasst. Ist er gedrückt, wird diese Automatik ausgeschaltet.

• Mit dem Button "Einstellungen" gelangt man zu einem erweiterten Einstellfenster für die Binomialverteilung und die automatische Einstellung der Achsen des Koordinatensystems (siehe rechts).

2. Die Felder "Punkte" und "Histogramm"

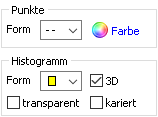
• Im Feld Punkte lassen sich die mit der Binomialverteilung berechneten Punkte einzeichnen - man kann sie sehr schön mit den senkrechten Linien (Histogramm) kombinieren.
• Im Feld Histogramm wählt man als Darstellung senkrechte Linien, schmale Rechtecke, Rechtecke mit der Breite 1 oder ein Liniendiagramm. Die Rechtecke werden mit einem Häkchen vor dem Feld "3D" als Quader dargestellt.

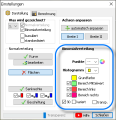
3. Das Feld zur Berechnung der Binomialverteilung

Die Genauigkeit entspricht exakt den ablesbaren Tabellenwerten einer Formelsammlung und macht damit die Verwendung der Tabellen einer Formelsammlung überflüssig!

• Zunächst gibt man im oberen Teil dieses Feldes die Anzahl n der Versuche und die Trefferwahrscheinlichkeit p ein. Der Erwartungswert µ und die Standardabweichung σ werden berechnet.
  Die Verteilung wird gezeichnet, dabei werden die Grenzen des Koordinatensystems automatisch an diese Verteilung angepasst.
  Mit einem Häkchen kann man den Bereich hervorheben, in dem der Erwartungswert liegt, daneben stellt man die Farbe dieses Bereichs ein.
  
  
• Im mittleren blauen Teil des Feldes legt man die Rechengenauigkeit fest:
  • Setzt man ein Häkchen bei "+1 Dezimale", erhöht sich die Rechengenauigkeit gegenüber den üblichen ablesbaren Tabellenwerten einer Formelsammlung um eine Stelle.
  • Setzt man ein Häkchen bei "Korrektur ±0,5", wird die Näherung verbessert, indem beim Berechnen von P(X≤3) die Näherung mit 3,5 statt mit 3 und bei P(X≥9) die Näherung mit 8,5 statt mit 9 berechnet wird.
• Im etwas helleren Rechenfeld darunter gibt man die Grenzen k₁ und k₂ der Bereiche an, dabei erfolgt die Eingabe entweder
  • direkt durch die Eingabe der Zahlen oder
  • durch den Schieberegler - oben verschiebt man den linken Bereich, unten den rechten Bereich.
• Die Wahrscheinlichkeiten P(X≤k₁), P(X≥k₂) und P(k₁+1≤X≤k₂-1) werden berechnet.
  Diese Wahrscheinlichkeiten lassen sich auf zwei Arten berechnen:
  Mit den Reitern "Binomialverteilung" und "Näherungsformel von de Moivre-Laplace" wählt man das Verfahren, mit dem die Wahrscheinlichkeiten berechnet werden.
  Verwendet man die Näherungsformel von de Moivre-Laplace, sollte man für eine optimale Näherung ein Häkchen bei "Korrektur ±0,5" setzen (So wird beim Berechnen von P(X≤3) die Näherung mit 3,5 statt mit 3 und bei P(X≥9) die Näherung mit 8,5 statt mit 9 berechnet.).