MatheGrafix 12 / Online-Hilfe

Zwei Rechenverfahren beim Testen von Hypothesen (z.B. beidseitiger Test)

Bei der Bestimmung des Ablehnungs- oder Verwerfungsbereich eines Hypothesentests werden zwei Verfahren verwendet, die allerdings nicht immer im Ergebnis übereinstimmen!
Zur Erläuterung der beiden Verfahren dient das 3. Beispiel (im Beispielfeld des linken Fensters von MatheGrafix): ein beidseitiger Test mit n = 80, H₀: p = 2/3 und α = 5%.

1. Verfahren mit Hilfe der Tabelle der summierten Binomialverteilung:
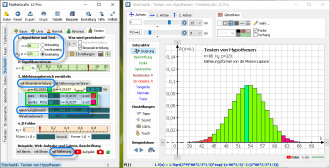   Man sucht in der Tabelle der summierten Binomialverteilung jeweils einen Wert für die Grenzen des linken und rechten Ablehnungsbereiches unter den Bedingungen:
   • P(X ≥ linke_Grenze des rechten Ablehnungsbereiches) ≤ α/2 = 2,5%
   • P(X ≤ rechte_Grenze des linken Ablehnungsbereiches) ≤ α/2 = 2,5%
   Dieses Verfahren verwendet MatheGrafix, wenn der Reiter "mit Binomialverteilung" ausgewählt wird.
   Bei diesem Beispiel erhält man den Ablehnungsbereich {0,...,44} ∪ {62,...,80}.
   Der exakte α-Fehler ist hier 4,34%.
   Die Darstellung der Binomialverteilung erfolgt als Säulendiagramm, bei dem der Ablehnungsbereich farbig abgegrenzt wird.


2. Verfahren mit der Näherungsformel von de Moivre-Laplace mit der Näherung über die Normalverteilung
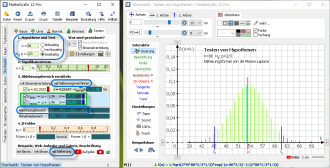   Hier werden die Grenzen c_links des linken und c_rechts des rechten Ablehnungsbereichs berechnet, wobei
   c_l = µ-1,96σ und c_r = µ+1,96σ ist.
   
   Dieses Verfahren verwendet MatheGrafix, wenn der Reiter "mit Näherungsverfahren" ausgewählt wird.
   Bei diesem Beispiel erhält man einen anderen Ablehnungsbereich {0,...,45} ∪ {62,...,80}.
   Der exakte α-Fehler ist dann 5,72%.
   
   Die Darstellung der Binomialverteilung erfolgt als Stabdiagramm: Nur so sieht man, wie die Senkrechten bei c_links und c_rechts die Bereiche trennen!

Beispiele

1. Beispiel: Rechtsseitiger Test mit n = 50, H₀: p ≤ 0,7 und α = 7%.
   
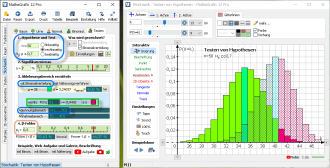   Mit der Tabelle der Binomialverteilung wird der Ablehnungsbereich gesucht, wobei der Ablehnungsbereich rechts ist und
   P(X ≥ linke_Grenze) ≤ α bestimmt wird.
   Der exakte α-Fehler wird berechnet, er beträgt bei diesem Verfahren 4,02% (Beim Näherungsverfahren über die Normalverteilung ist der exakte α-Fehler 7,89%.).
   Für die alternative Hypothese mit p₁ = 0,8 wird der β-Fehler ebenfalls über die Tabelle der Binomialverteilung berechnet.
   
   Die Darstellung der Binomialverteilung mit n = 50 und p₀ = 0,7 erfolgt über gefüllte Rechtecke.
   Die Darstellung der alternativen Binomialverteilung mit n = 50 und p₁ = 0,8 wird visualisiert über halb durchsichtige Rechtecke, die vor der ersten Verteilung liegen.
   
   
2. Beispiel: Linksseitiger Test mit n = 50, H₀: p ≥ 1/3 und α = 7%.
   
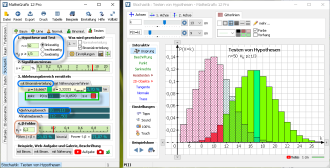   Mit der Tabelle der Binomialverteilung wird wieder der Ablehnungsbereich gesucht, wobei hier der Ablehnungsbereich links ist und
   P(X ≤ rechte_Grenze) ≤ α bestimmt wird.
   Der exakte α-Fehler wird berechnet, er beträgt bei diesem Verfahren 5,70%.
   Für die alternative Hypothese mit p₁ = 0,2 wird der β-Fehler ebenfalls über die Tabelle der Binomialverteilung berechnet.
   
   Die Darstellung der Binomialverteilung mit n = 50 und p₀ = 0,7 erfolgt über gefüllte Rechtecke.
   Die Darstellung der alternativen Binomialverteilung mit n = 50 und p₁ = 0,2 wird visualisiert über halb durchsichtige Rechtecke, die vor der ersten Verteilung liegen.
   
   

Einstellungen beim Testen von Hypothesen

Im Modul "Testen von Hypothesen" erfolgen viele Einstellungen automatisch, z.B. die Anpassung der Verteilung an die Achsen oder die Darstellung der Binomialverteilung als Stab- oder Säulendiagramm.

Im linken Fenster gelangt man über den Button "Einstellungen" zu weiteren Anpassungsmöglichkeiten, insbesondere zur Farbgebung oder zur Darstellung der Verteilung als Stabdiagramm, Säulendiagramm oder mit Quadern.