MatheGrafix 12 / Online-Hilfe

Aufgabe: Rechtsseitiger Test, Berechnung des Ablehnungsbereichs

Von den in einem Betrieb gefertigten Glühlampen haben 25% eine Brenndauer von weniger als 6000 Stunden. Durch ein neuartiges Herstellungsverfahren soll die Qualität verbessert werden. Aus der neuen Fertigung werden 100 Glühlampen entnommen. Wie viele davon müssen mindestens mehr als 6000 Stunden brennen, damit man das neue Verfahren mit einer Irrtumswahrscheinlichkeit von höchstens 5 % als besser bezeichnen kann?

Lösung

Bestimmung des Ablehnungsbereichs mit den Tabellen der Binomialverteilung und mit der Näherungsformel von de Moivre-Laplace:

• Stichprobenumfang: n = 100
• Treffer bedeutet: Die Glühlampe brennt mindestens 6000 Stunden.
• Zufallsgröße X: Anzahl der Treffer bzw. Anzahl der Glühlampen, die mindestens 6000 Stunden brennen.
• X ist bei wahrer Nullhypothese B_100;0,75-verteilt.
• Die Hypothesen lauten: H₀:p ≤ 0,75 (die Qualität sei geblieben) und H₁:p > 0,75.
  Da große Werte von X gegen H₀ sprechen, handelt es sich um einen rechtsseitigen Test.
• Vorgegebenes Signifikanzniveau: α = 5%
  
  
• Bestimmung des Ablehnungsbereichs:
  
  
  • Methode 1: Lösung mit den Tabellen der Binomialverteilung
    
    
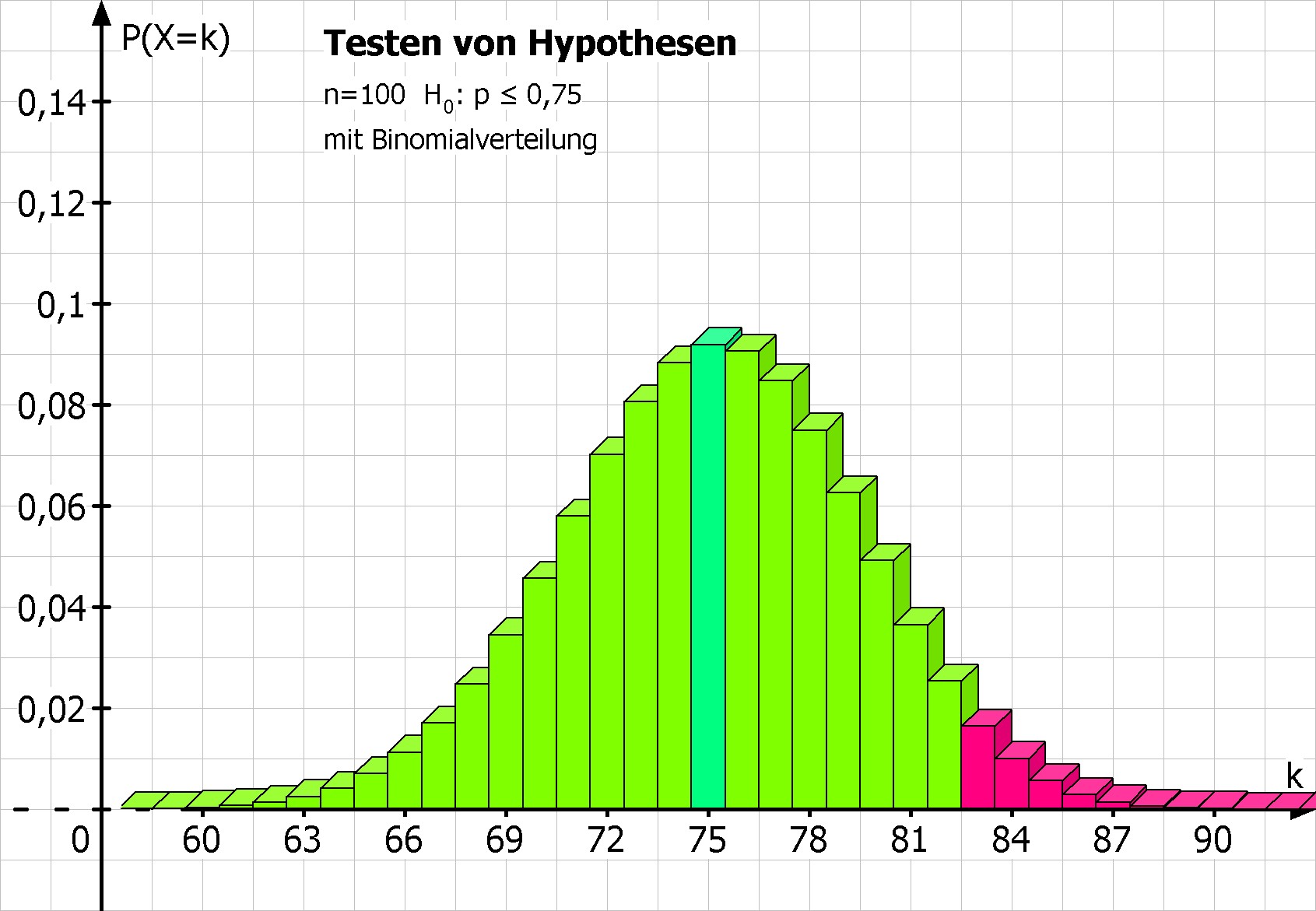
    Gesucht ist die kleinste Trefferzahl k mit P(X≥k) = 1-P(X≤k-1) ≤ 5% = α.
    MatheGrafix liefert den Ablehnungsbereich {83,84,85, ... ,100}.
    Der genaue Wert für α ist bei dieser Methode 3,76%.
    
    Bild links: Diese Darstellung wird von MatheGrafix automatisch generiert. MatheGrafix berechnet den Ablehnungsbereich von 83 bis 100.
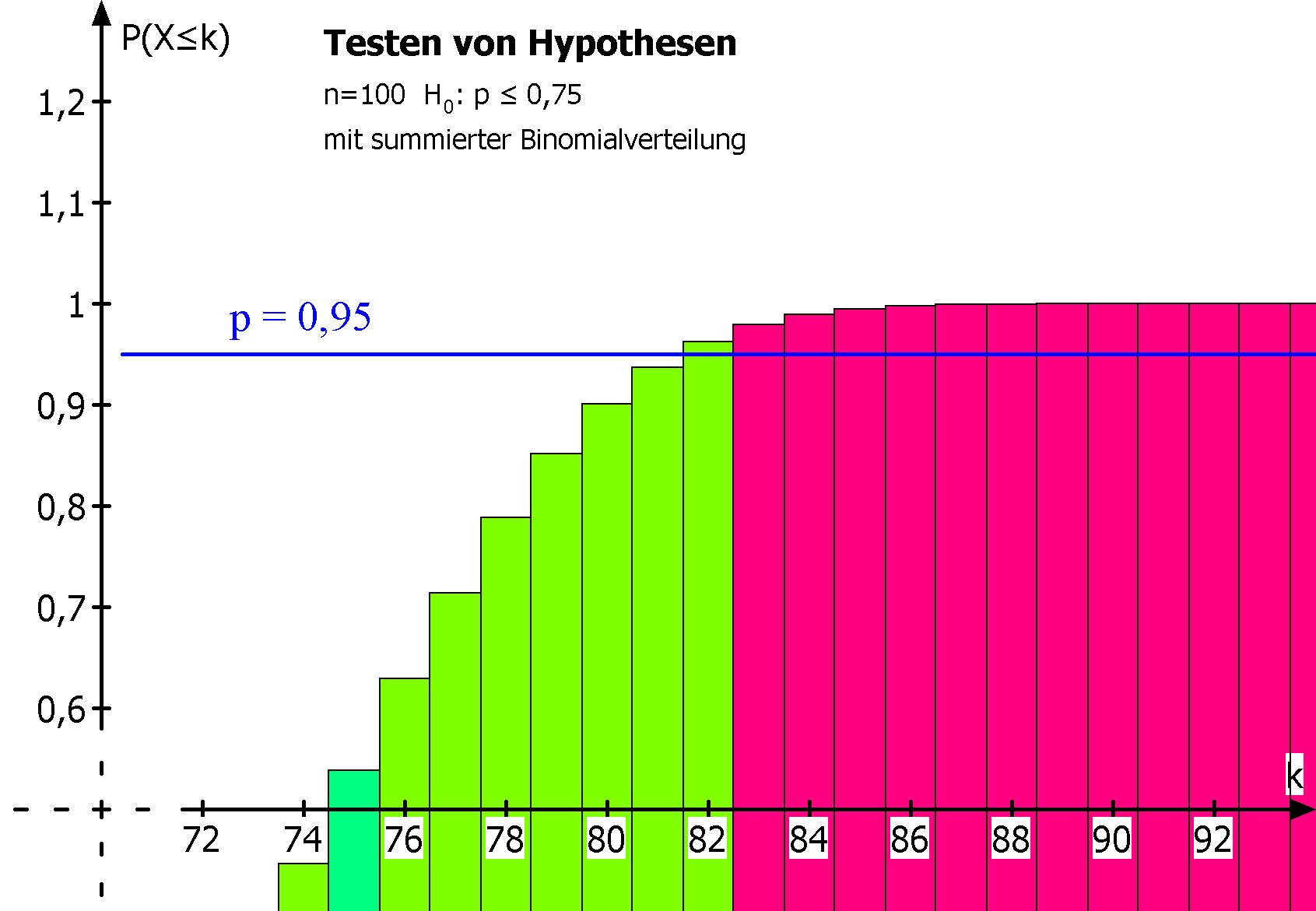
    Bild rechts: Bei der summierten Binomialverteilung wurde die Grenze p = 0,95 = 1-α eingezeichnet.
    Warum trennt nun diese Grenze nicht die Bereiche auf dem Bild?
    P(Annahmebereich) darf dabei nicht unter dieser Grenze liegen, da sonst P(Ablehnungsbereich) > 5% wird.
    In Formeln: Aus P(X≥k) = 1-P(X≤k-1) ≤ 5% folgt ja P(X≤k-1) ≥ 0,95: Auf dem Bild sieht man P(X≤82) ≥ 0,95, also ist k-1=82 und damit k=83.
    
    
  • Methode 2: Lösung mit der Näherungsformel von de Moivre-Laplace
    
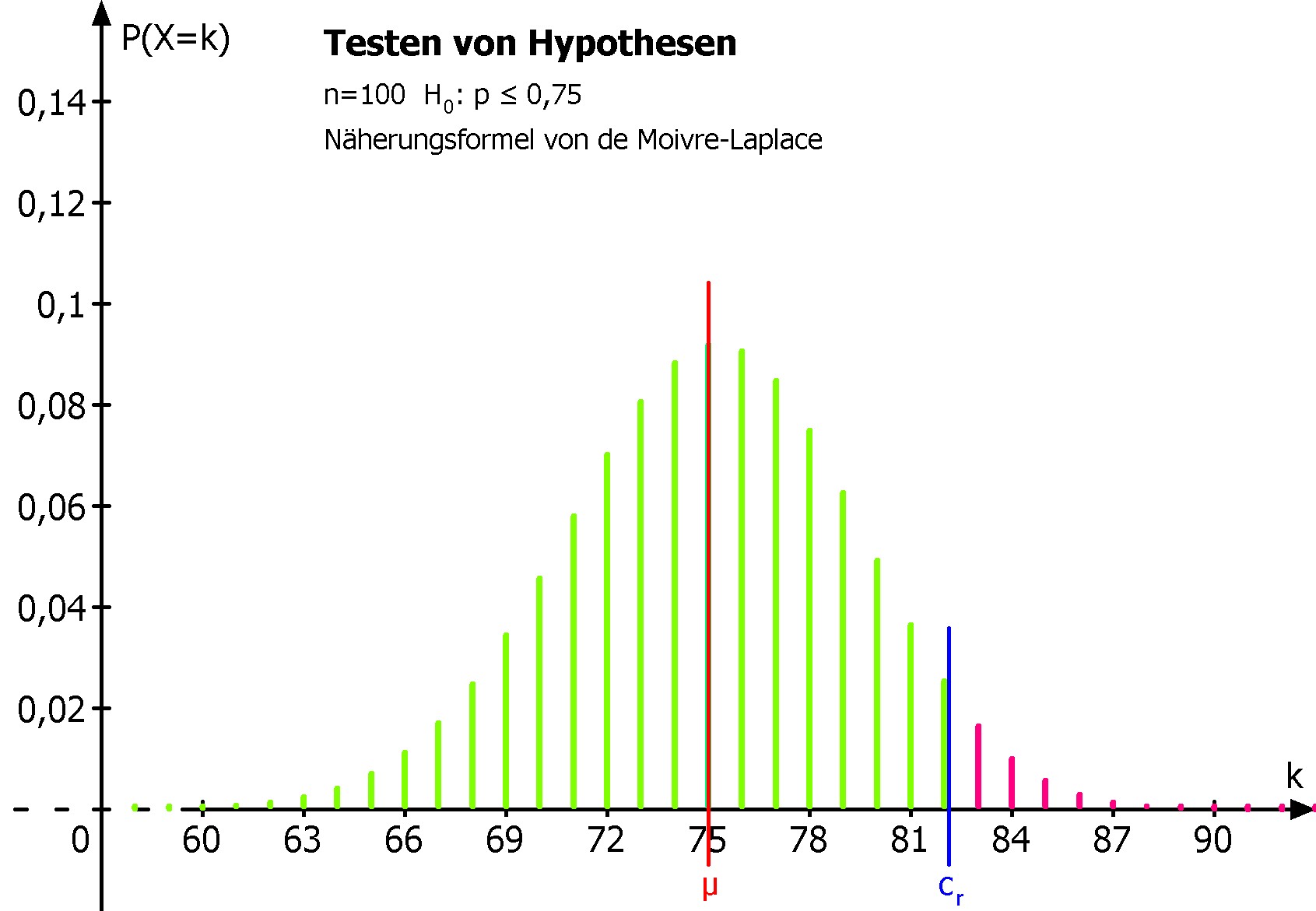    Man berechnet die Grenze c_rechts = µ + 1,64*σ = 82,12, diese trennt den Ablehnungsbereich und den Annahmebereich.
    MatheGrafix liefert mit dieser Methode ebenfalls den Ablehnungsbereich {83,84,85, ... ,100}.
    
    Bild: Bei dieser Methode trennt die Senkrechte bei c_rechts den Ablehnungsbereich und den Annahmebereich. Die Darstellung mit Rechtecken oder Quadern eignet sich hier nicht, daher wird die Binomialverteilung als Stabdiagramm dargestellt.

Ergebnis: Brennen mehr als 82 Lampen länger als 6000 Stunden, kann das neuartige Herstellungsverfahren mit einer Irrtumswahrscheinlichkeit von 5% als besser bezeichnet werden.

Download MatheGrafix-Dateien

Lösung: Ablehnungsbereich Binomialverteilung
Lösung: Ablehnungsbereich summierte Binomialverteilung
Lösung: Ablehnungsbereich Näherungsformel

Download Webseite als Word-Text

Testen von Hypothesen: Aufgaben und Lösungen